Las Leyes de los Logaritmos son propiedades que tienen las funciones logarítmicas y tienen sus bases en las leyes de los exponentes. Para cualquier logaritmo, existen las siguientes leyes que se pueden aplicar:
Logaritmo de un Producto: Sean A y B dos números reales positivos. El logaritmo del producto de A y B es igual a la suma de los logaritmos de cada factor, es decir:
Logₐ(AB) = LogₐA + LogₐB
Logaritmo de un cociente: Sean A y B dos números reales positivos. El cociente de A y B es igual a la resta de los factores, es decir:
Logₐ(A/B) = LogₐA - LogₐB
Logaritmo de una potencia: Sea A un número real positivo y n un exponente real positivo. El Logaritmo de A elevado a la potencia n, es igual a multiplicar n por el logaritmo de A, es decir:
Logₐ(Aⁿ) = (n)LogₐA
Logaritmo de una raíz: Sea A un número real positivo, El logaritmo de la raíz cuadrada de A es igual a dividir el logaritmo de A entre la raíz enésima.
Logₐ(a1/n) = (LogₐA)/n
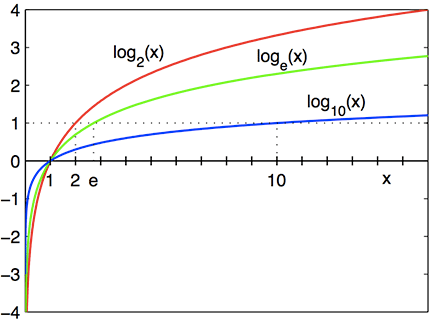
Tabla de contenidos
Ejemplos de las Leyes de los Logaritmos
De acuerdo a las anteriores leyes de los logarimos, podemos escribir algunos ejemplos de uso como los que vienen a continuación:
Ejemplos de logaritmo de un producto (asumiendo un logaritmo base 10, evitamos escribir la base “a” existente en la explicación, sin embargo puede aplicarse la misma regla a cualquier base:
log[(10)(1000)] = log(10) + log(1000) = 1 + 3 = 4 log(10x) = log(10) + log(x) = 1 + log(x)
Ejemplos de logaritmo de un cociente:
log(100/10) = log(100) - log(10) = 2 - 1 = 1 log(10/x) = log(10) - log(x) = 1 - log(x)
Ejemplos de logaritmo de una potencia:
log(10^100) = (100)log(10) = 100(1) = 100 log(100^x) = (x)log(100) = (x)(2) = 2x
Demostración de las Leyes de los Logaritmos
El logaritmo es una función que tiene como objetivo calcular el exponente necesario que requiere un número base para llegar al valor del logaritmo. Ésto significa los siguiente:
Logₐ(B) = C
Donde: a es la base del logaritmo, B es el Argumento, antilogaritmo o valor para el que buscamos el exponente, y C es el valor del logaritmo o exponente deseado. Ésto significa lo siguiente:
Si queremos calcular logₐ(100), el valor de la base “a” es 10 (es decir log(100), “a” no se escribe), y su interpretación se podría pronunciar así: “Queremos calcular el valor del exponente por el cuál 10 es igual a 100”. Es decir:
log(100) = 2
Lo anterior significa que el exponente necesario para llegar de 10 a 100, es 2, es decir
10^2 = 100
Lo cual es válido, porque (10)(10) = 100.
Demostración de algunas propiedades
Algunas de las propiedades obtenidas de las leyes de los logaritmos, y sus respectivas demostraciones, son las siguientes:
logₐ(1) = 0
Demostración:
Si logₐ(1) = c, entonces a^c = 1
Como todo número elevado a la potencia cero da como resultado 1, entonces c = 0.
a^logₐ(b) = b
Demostración:
Sea logₐ(b) = c, entonces a^c = b
Por otro lado a^logₐ(b) = a^c = b
Y por la propiedad de transitividad concluimos que a^logₐ(b) = b
logₐ(bc) = logₐ(b) + logₐ(c)
Demostración:
Sea logₐ(bc) = d, entonces a^d = bc
*) Si logₐ(b) = e, entonces por definición de logaritmo, a^e = b
**) Por otro lado, si logₐ(c) = f, entonces a^f = c
Multiplicando * y **, entonces tenemos que (a^e)(a^f) = bc
bc = a^(e+f) = bc
Sustituyendo * en ésta ecuación:
a^(e+f) = bc = a^d
Como a^(e+f) = a^d => e + f = d, entonces al usar las definiciones, deducimos que:
logₐ(b) + logₐ(c) = logₐ(bc)
Logₐ(b/c) = logₐ(b) - logₐ(c)
Demostración:
Sea logₐ(b/c) = d, y usando la definición de logaritmo esto significa: a^d = b/c
Sean logₐ(b) = e, logₐ(c) = f
Entonces a^f = c
Dividimos a^e/a^f = b/c
Entonces a^(e-f) = b/c = a^d
Y por transitividad a^(e-f) = a^d => e-f = d
Y utilizando las ecuaciones anteriores, deducimos que:
logₐ(b) - logₐ(c) = logₐ(b/c)
Con lo anterior hemos demostrado algunas de las leyes de los logaritmos, sin embargo existen muchos problemas diferentes, los cuáles tienen demostraciones en cada caso.
Leyes de Logaritmos en otras bases
Aún cuando los ejemplos se hicieron utilizando la base 10, las leyes de los logaritmos aplican para todas las bases, entre las más comunes, tenemos los logaritmos base 2, base e (también llamado logaritmo natural) y otras bases.
Al final la base es lo de menos, y por eso las demostraciones de las leyes de los logaritmos se hacen con logaritmos base n, es decir, puede tratarse de cualquier base (número entero mayor a cero).
Otros temas interesantes
Puedes también aprender contenidos de otros temas interesantes, por ejemplo el cálculo de Pi, o bien las series de Taylor. Para ingresar solo da click en los enlaces.